Test auf Normalverteilung
Viele statistische Verfahren setzen voraus, daß die Daten (der Stichprobe) zumindest annähernd normalverteilt sind. Um diese Voraussetzung zu prüfen, bietet SPSS im Menü "Deskriptive Statistik|Explorative Datenanalyse" zwei statistische Testmöglichkeiten. Darüber hinaus sind in einige andere Analyseprozeduren Tests auf Normalverteilung integriert.
Es gibt allerdings kaum eindeutige Kriterien, ab wann eine Abweichung von der Normalverteilung ein statistisches Verfahren wirklich stört. Bedenklich werden Abweichungen jedenfalls dann, wenn eine Verteilung sehr schief oder mehrgipflig ist.
Inhaltsverzeichnis
Kolmogorov-Smirnov-Test
Der Kolmogorov-Smirnov-Test kann unter "Explorative Datenanalyse..." ausgewählt werden, indem man auf "Diagramme" klickt und dann "Normalverteilungsdiagramm mit Tests" markiert. Relevant für die Interpretation ist die Angabe bei "Signifikanz". Je kleiner dieser Wert ist, desto unwahrscheinlicher ist eine Normalverteilung. Wenn SPSS hier .000 ausgibt, sollte auf jeden Fall Abstand von einer Annahme der Normalverteilung genommen werden.
Shapiro-Wilk-Test
Die Interpretation dieses Tests funktioniert genau wie die des Kolmogorov-Smirnov-Tests. Wenn die Zahl unter Signifikanz sehr klein oder gar .000 ist, kann man nicht vom Vorliegen einer Normalverteilung ausgehen.
Sichtprüfung mit Graphiken
Die beiden statistischen Tests werden in der Literatur kaum behandelt und sind offenbar nicht besonders bedeutend. Einer anderen Vorgehensweise zum Test auf Normalverteilung wird dagegen große Bedeutung zugemessen: Dem einfachen Sichtvergleich einer Graphik der Stichprobendaten mit einem Bild einer Normalverteilung. Ist die Ähnlichkeit hinreichend groß (das heißt in den meisten Fällen: Ähnlichkeit mit einer symmetrischen, eingipfligen Glockenkurve), kann man davon ausgehen, daß die Anforderung "normalverteilt" erfüllt ist.
Histogramm bei der Häufigkeitsauszählung
Bei einer Häufigkeitsauszählung kann mit Hilfe der Schaltfläche "Diagramme" eingestellt werden, daß ein "Histogramm mit Normalverteilungskurve" ausgegeben werden soll. Das Ergebnis sieht dann z.B. folgendermaßen aus:
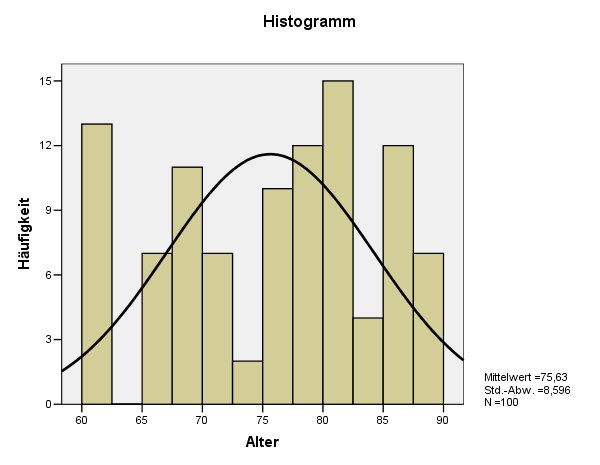
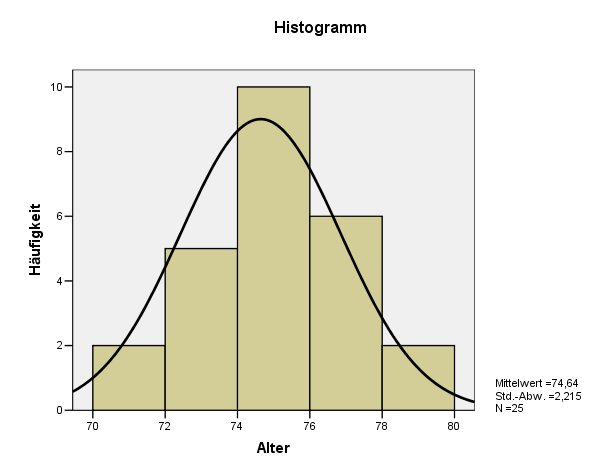
Das erste Bild zeigt eine mehrgipflige Verteilung, die keine Ähnlichkeit mit der Normalverteilung hat. Kolmogorov-Smirnov-Test und Shapiro-Wilk-Test ergeben für diese Daten eine Signifikanz von .000, bestätigen also den optischen Eindruck, daß hier keine Normalverteilung angenommen werden darf. Das zweite Bild ähnelt ganz offensichtlich einer Normalverteilung. Die Werte der beiden Tests sind für diese Daten deutlich größer als .000, allerdings kaum zu interpretieren. In solchen Fällen verlässt man sich besser auf den optischen Eindruck.
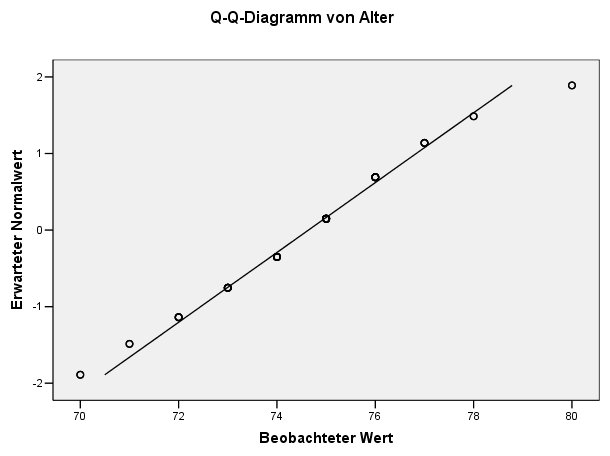
Q-Q-Diagramm und trendbereinigtes Q-Q-Diagramm
Unter "Deskriptive Statistiken|Explorative Datenanalyse..." werden zusammen mit den beiden statistischen Tests auch zwei Graphiken mit ausgegeben. Die erste Graphik ist ein Q-Q-Diagramm, das die Meßwerte mit einer Gerade vergleicht, die eine Normalverteilung repräsentiert. Streuen die Werte eng und zufällig um die Gerade, kann man eine Normalverteilung der Daten annehmen.
Die zweite Graphik, die SPSS zusammen mit den beiden statistischen Tests ausgibt (trendbereinigtes Q-Q-Diagramm), erfüllt einen ähnlichen Zweck wie die erste, nur daß die Linie, die die Normalverteilung repräsentiert, nun horizontal ist. Die besten Aussichten auf normalverteilte Daten hat man, wenn die Daten zufällig und ohne Muster um die horizontale Linie streuen.